没有上下文的数字用途非常有限。因此,在更广阔的世界中,报纸和报道中的文章经常会将它们传递的数字与 (平均) 平均值进行比较,这是一件好事。但是,这始终不足以衡量所报告的数据真正告诉我们的内容。有一个古老的 “笑话”,讲的是一名统计学家淹死在平均深度只有几英寸的湖中 (确切的平均深度似乎取决于谁在讲笑话),但仅仅通过报告或与平均值进行比较来过度简化确实会产生很大的误导。
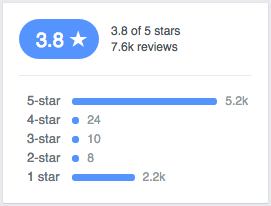
在撰写本文时,爱尔兰共和国都柏林的White Moose caf é 在Facebook上的评分为3.8星 (满分5星)。从这个数字来看,如果不看分数的分布,你可能会认为这意味着 “人们通常认为这是一个很好的咖啡馆,也许可以做一些改进,把它提高到4星以上”。事实上,该机构有超过7,000条评论,但只有42位评论者给了它2星,3星或4星评级!绝大多数评级是1星或5星。这种两极分化的观点的极端例子是业主与素食主义者之间分歧的结果,最初导致许多素食主义者的负面评论遭到轰炸,随后又遭到肉食者的强烈反对; 可以肯定地说,大多数评论者从未去过咖啡馆。(你可以在这里找到更多关于这个故事的信息。)平均评分并没有给我们任何潜在故事的暗示。
所以希望你能明白为什么不仅仅是报告 (平均值) 平均值或将一个结果与平均值进行比较是一个好主意。我们还有很多其他描述性统计数据可以告诉我们更多关于一组结果的分布: 中位数,模式,标准差,方差,偏斜,峰度,范围,四分位数范围…但通常最好的选择是可视化结果。Facebook实际上确实通过其审查系统做到了这一点,如下面的屏幕截图所示:
Anscombe的quartet是一个典型的例子,说明了可视化的需求: 一组四个成对的x和y值的小数据集。所有四个数据集在x变量中具有相同的均值 (9) 和方差 (11),在y变量中具有几乎相同的均值 (〜7.5) 和方差 (〜4.12)。每个数据集的相关系数也相同 (0.82) 到小数点后两位。实际上,将数据绘制为一组简单的散点图突出显示了四个数据集实际上非常不同。
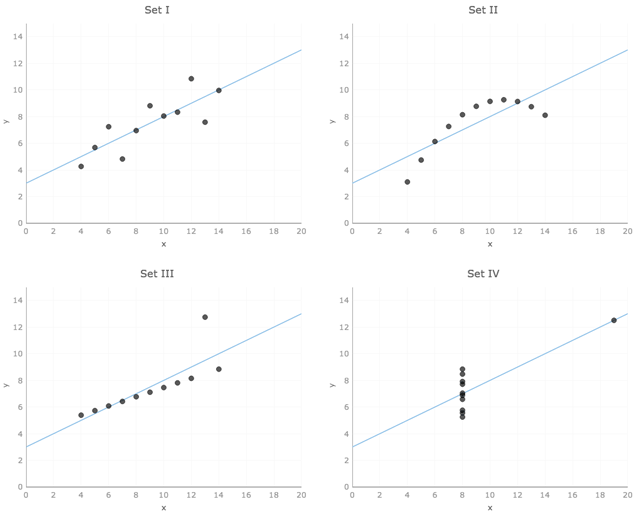
也许最令人惊讶的是,每组的线性回归线 (几乎) 相同。这是一个垃圾输入,垃圾输出的情况; 如果你试图拟合一条直线来显示一个变量如何影响另一个变量,并且关系甚至不接近线性,那么不要指望你的线甚至远程代表你的数据。当然,我们并不特别擅长以表格形式吸收和解释大量数据,因此set II不是线性的事实在电子表格中可能并不完全明显: 在尝试拟合数据之前绘制数据!
散点图是像Anscombe这样的配对数据集的明显选择。一维等效物是带状图。让我们使用Anscombe的y值作为一个简单的例子:
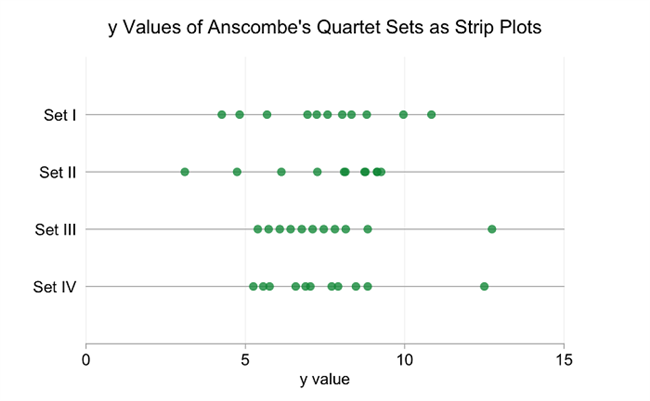
条形图很好地突出了集合III和集合IV中异常值的存在,并显示对于所有集合,大部分数据点位于5和10之间。
当每个集合只有适度数量的数据点时,条线图通常效果很好。有了更大的数据集,事情很快就会变得过于拥挤。可以尝试通过给每个点一个随机的垂直偏移来解决这个问题,以清除一些东西,基本上是将抖动添加到不存在的第二个变量,但更常见的替代方法是将数据装箱并创建直方图。例如,下面是由特定连续随机数生成器生成的300,000数据点构成的直方图。
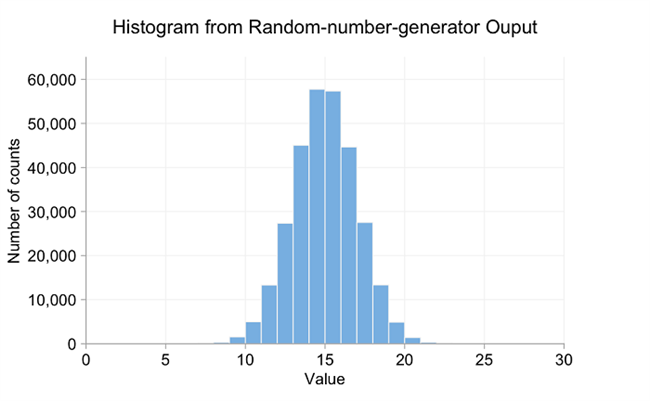
挑选适当的箱宽度是重要的。鉴于上图显示了连续的数据,您可以告诉您所使用的bin宽度确实是不必要的宽。而不是使用一个单位宽的垃圾箱,我们可以将其减少到0.1个单位宽。
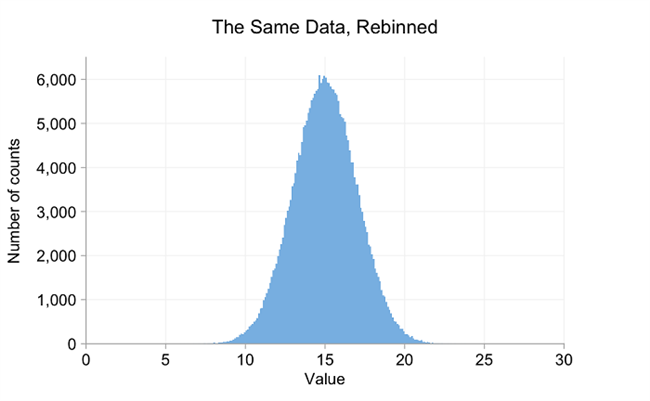
希望这使得随机数生成器从正态分布中提取数字更加明显。特定分布的平均值为15,标准偏差为2。在接下来的示例中,从不同的正态分布得出数字。
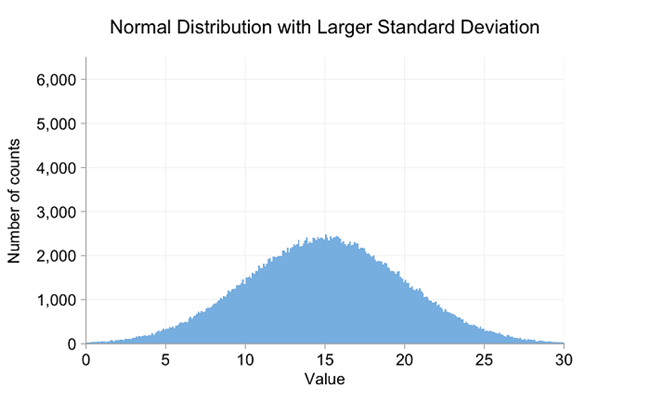
在这种情况下,正态分布的均值与前面的例子相同-15-但标准差要大得多-5。这意味着得到低于8或高于22的数字的概率比前面的例子高得多。但是,如果你只是引用意思,就无法说明这一点。
使用您喜欢的框架为任何场景创建现代Web应用程序。下载Ignite UI今天体验一下Infragistics jQuery控件的强大功能。
