我以前注意到 ,当传统的折线图是更好的选择时,我认为经常使用堆叠面积图。这是我以前使用的 (虚构的) 示例和常规的折线图。
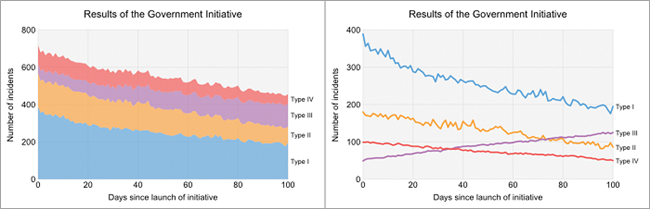
简而言之,如果你希望人们能够对单个组件的大小做出合理准确的判断,以及它们如何根据其他变量 (如时间) 而变化,那么传统的折线图设计几乎总是最好的选择。除了底部组件之外,所有组件都缺乏稳定的基线,这使得堆叠面积图难以完成此任务。
如果要说明随另一个变量变化的组件的有序总和,则堆叠面积图可能很有用。虽然以前我建议从农场到商店的牛奶生产成本可能随着时间的变化可能是合适的,但在这里我想考虑一些非常不同的东西: 选定的数学级数。
你可能熟悉三角函数,如正弦和余弦,你也可能知道指数函数和双曲函数。如果你有某种计算器,绘制这些函数的图形是相当容易的。当被束缚在复杂的方程中时,这些函数可能变得难以处理。因此,近似这些函数的替代方法可以非常方便。
上面提到的函数都是解析函数这是什么真正的意思是相当复杂的试图解释,所以我不会尝试这样做在这里。相反,我将坚持以下几点: 这些函数都可以写为其参数 (通常表示为x) 的幂之和,即多项式。明确的帮助,所以这里是重写指数函数的一种方式:
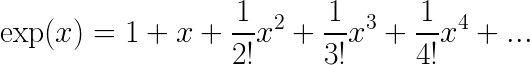
以类似的方式,这里是表达余弦函数的另一种方式:
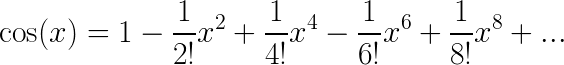
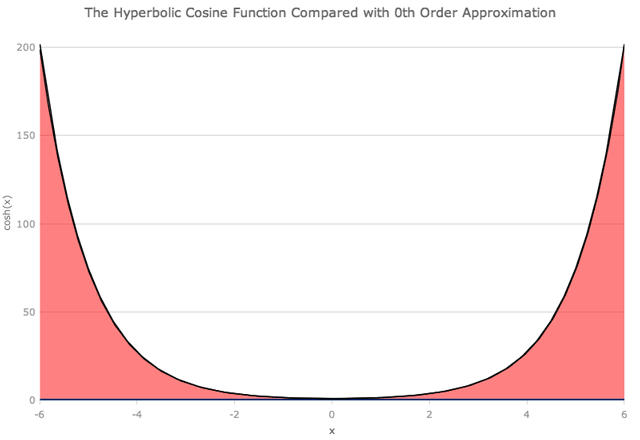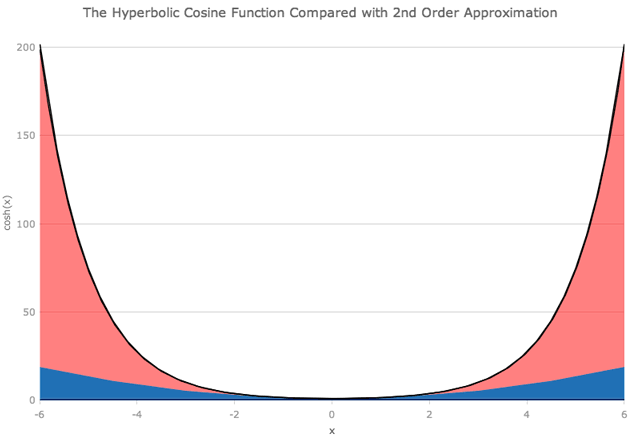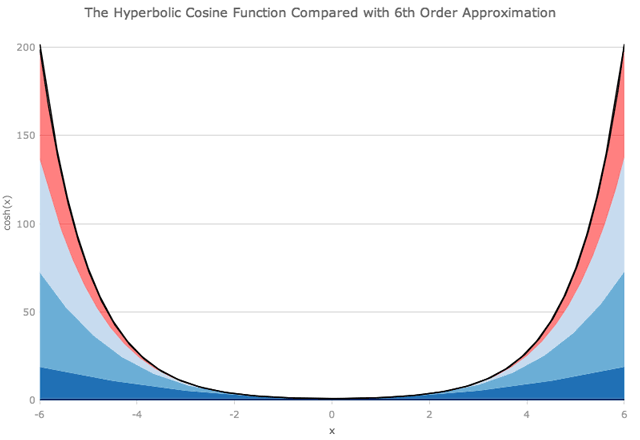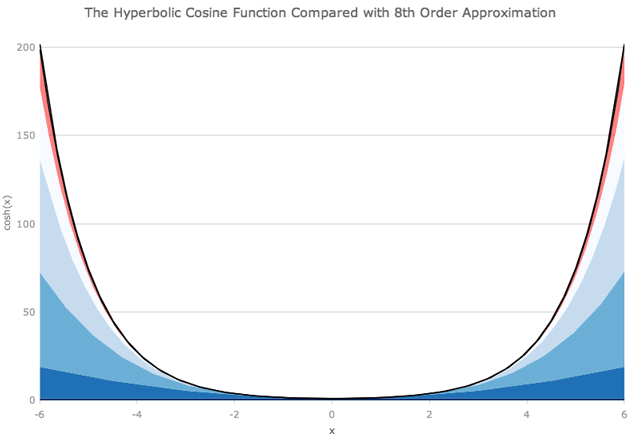
这里是双曲余弦函数 (通常写为cosh):
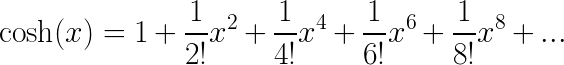
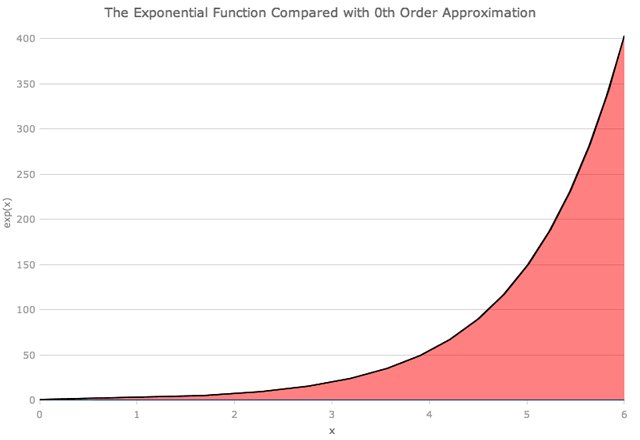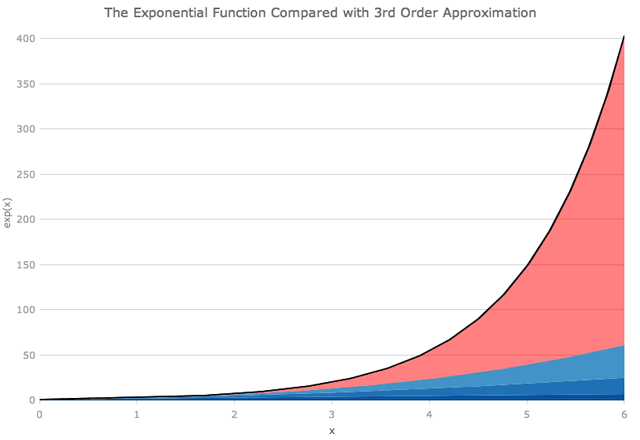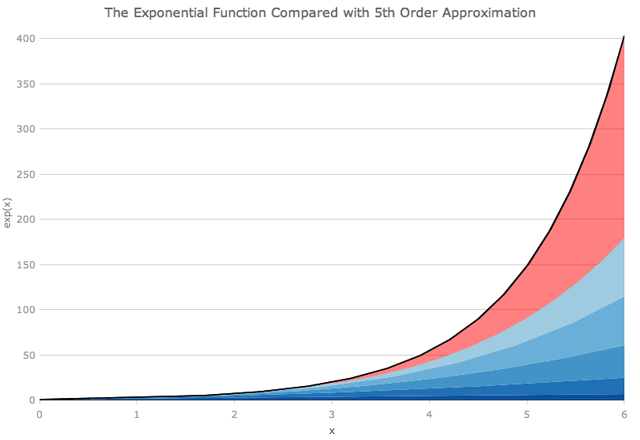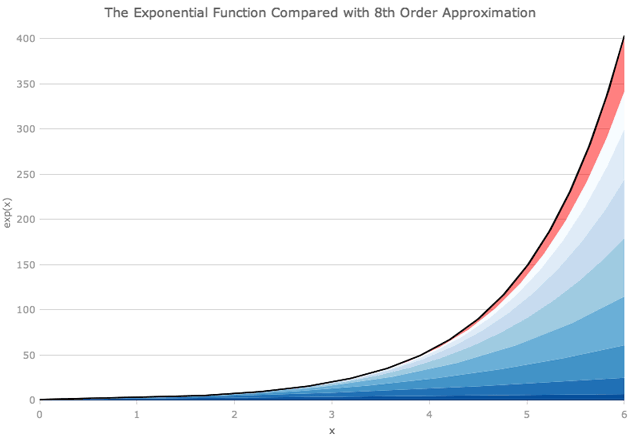
一般来说,要使用求和获得这些函数之一的精确值,我们需要求和到无穷大。在除了第一项之外的所有项都等于0的原点处,情况并非如此。接近原点,我们也将得到一个很好的近似值,因为x很小。但是有多近,有多好?我们可以绘制例如指数函数表达式的前几项,然后查看。下面GIF中的黑线显示了精确的指数函数,蓝色楔形显示了从方程右侧 (从x的零幂到8) 添加越来越多的项的结果。半透明的红色楔形表示多项式近似未覆盖的区域。
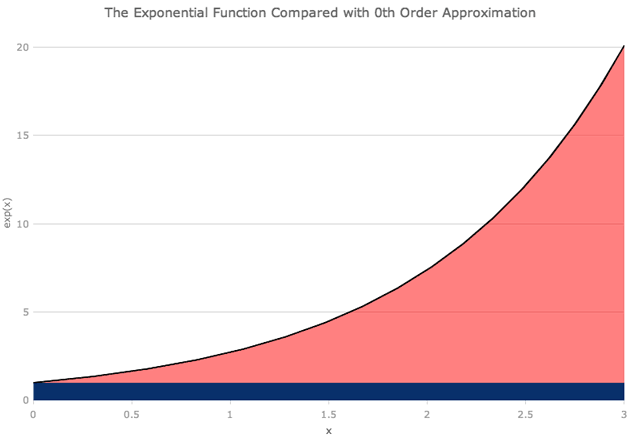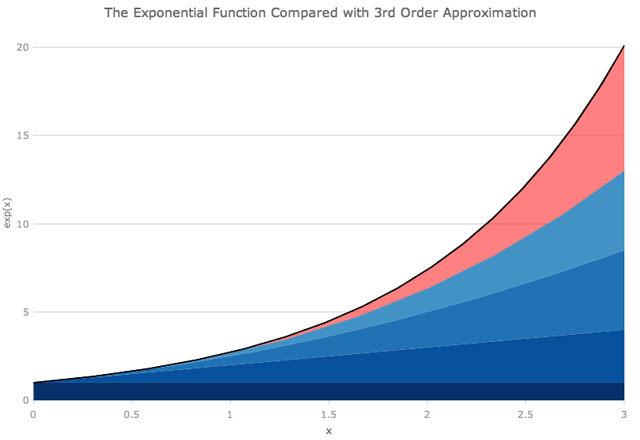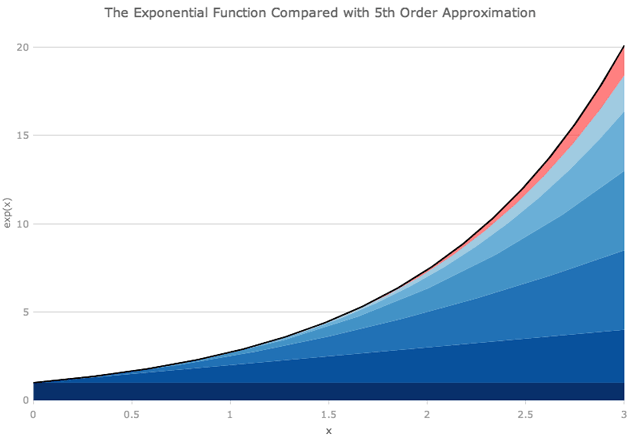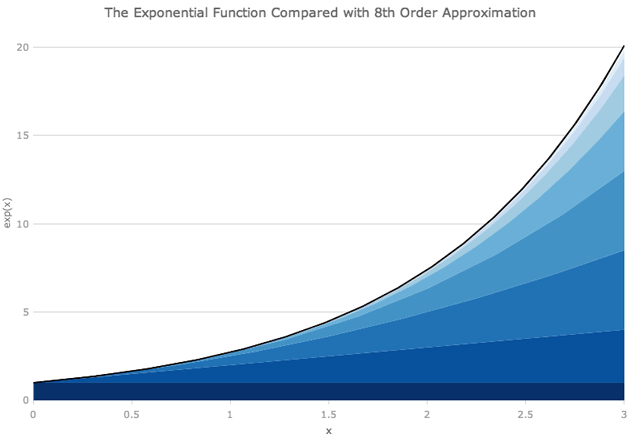
下面关于x = 1,我们可以看到多项式的前三项是指数函数的很好的近似值。为了在x = 3附近得到良好的近似,我们需要上升到x的六或七次幂 (即多项式的七或八项)。正如下面的GIF所示,即使在x = 6附近, x的八次幂也不够。
我们可以以类似的方式查看双曲余弦函数,尽管没有x的奇数次幂的项。
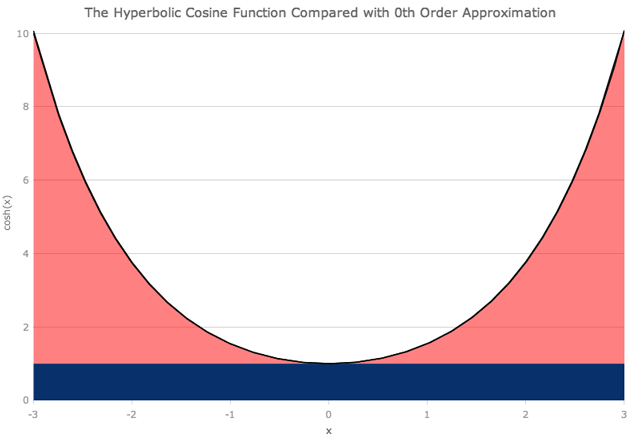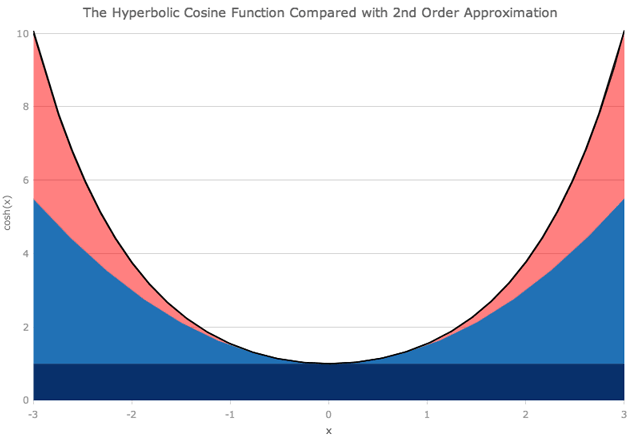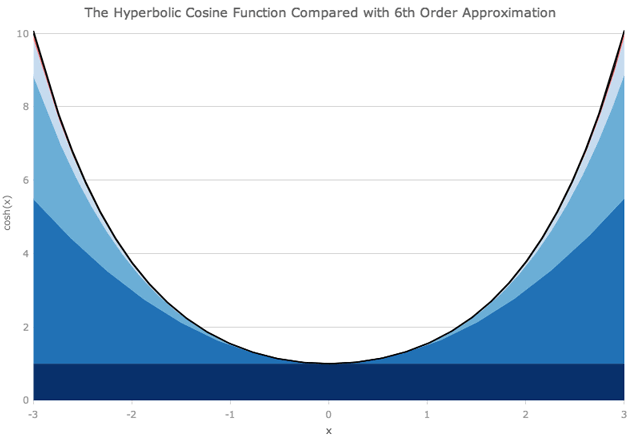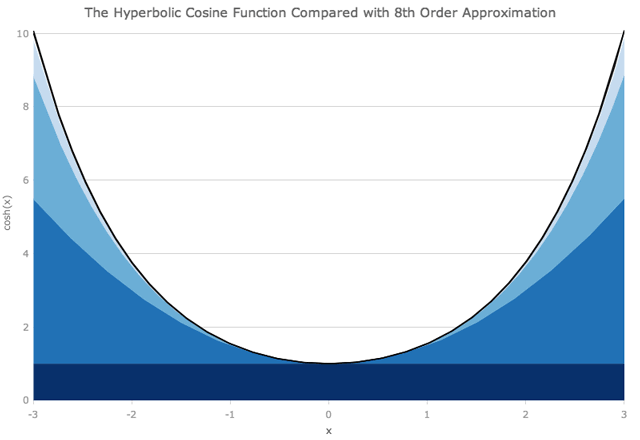
正如您可能期望的那样,当我们查看距原点较远的距离时,我们需要越来越多的多项式项,以便与确切的函数紧密匹配。在x = ± 6时,将项加到x的8次方不足以获得良好的近似。
我认为这些是堆叠面积图可以真正使用的情况。我们真正感兴趣的是组件的渐进总和,而不是单个部分,这就是堆叠图表的优势所在。
你可能注意到我跳过了为余弦函数生成图表。那是因为堆叠图失败了。为什么?因为连续的项有相反的符号。虽然在多项式近似中包含越来越多的项确实可以使您越来越接近确切的函数,但您不能将其显示为一个简单的堆栈,因为某些项会添加到总数中,而其他项会减去。当x为负时,这也是指数函数的问题: 涉及x的偶数次幂的项将为正,而涉及x的奇数次幂的项将为负。这是一个纯粹的视觉问题,当我们绘制线条而不是堆栈时不会出现。
希望我已经表明,堆叠面积图可以是有用的,当它是感兴趣的组件的有序总和,如果条件是正确的。为了使条件正确,则堆栈的所有组件必须在沿水平轴的每个 (可见) 点处共享相同的符号 (或为0)。
带来大量的复杂信息的生活与的Infragistics WPF强大的数据可视化功能! 下载免费试用现在!
