能够生成 (显然) 随机数是数学,统计学,科学,技术和游戏等许多领域的基本要求。例如,它们可用于将参与者分配到随机对照试验中的一组,以确定计算机游戏的输出或找到其他棘手问题的近似解决方案。我经常使用随机数来检查我的解决方案,以完美易处理的统计问题。加密随机数生成器,我们不会在这里介绍,可以在安全中使用。
类型的随机数生成器
至少就本文而言,我们可以想到有三类随机数集合:
- “真” 随机数;
- 伪随机数;
- 准随机序列。
真实 (或硬件) 随机数生成器 (trng) 使用被认为本质上是随机的真实世界的物理过程来创建数字流。例如,来自放射源的衰变事件是随机的并且彼此不相关,也可以使用大气噪声。
对于许多目的来说,trng通常是不实用或不方便 (或不必要) 的。一个更常见的替代方法是使用计算机算法创建一个数字流,这些数字流似乎在某个时间间隔内随机分布。这些算法不是真正不可预测的,因此被称为伪随机数发生器 (prng)。
最后,准随机序列是数字的有限集合,旨在以某种方式代表样本空间。例如,序列的平均值可以与群体的已知平均值相同 (或非常相似)。虽然准随机序列很有趣并且可能很有用,但它们不是本文的重点,因此将不再进一步讨论。
标准均匀分布
通常,来自伪随机数生成器的大量值的输出意味着近似覆盖范围0到1的标准均匀分布 (SUD)。然而,在是否包括端点中的任一个/两个方面存在一些变化。在连续分布数学的概念世界中,[0,1] 之间的均匀分布 (包括0和1) 与 (0,1) 之间的均匀分布 (不包括0和1) 之间的均匀分布基本上没有区别。在浮点数的现实世界中,只有有限数量的0和1之间的可能值,差异是真实的,可能是有问题的。例如,可能希望在自然对数函数Math.log中使用生成的数字。
为另一个分布生成随机数通常 “只是” 使用来自SUD PRNG的一个或多个数字来从感兴趣的分布产生适当的值。根据所需的最终分布,这可能涉及一行代码或相当复杂的东西。对于本文的其余部分,我将继续讨论从SUD PRNG生成数字。
期间
一个有用的PRNG必须有一个大的周期,也就是说它必须能够输出大量的数字而不会重复自己。例如,Wichmann Hill PRNG 1982年 (稍后将详细介绍) 的周期接近7万亿个数字,而非常受欢迎的Mersenne Twister PRNG的周期为2 19937 -1个数字。按照现代标准,前者被认为是相当短的。
有什么问题数学.随机?
您可以定期使用JavaScript内置的Math.random ,并且没有任何问题。然而,它有一个很大的限制: 它的输出是不可复制的。一次又一次地运行Math.random代码,每次都会得到一组不同的结果。在许多情况下,这真的不是问题。事实上,在许多 (大多数,可能) 情况下,它会正是你想要的。不可预测性 (至少对于盯着输出的人来说) 正是所需要的。但有时我们确实希望看到同样的结果。
暂时远离JavaScript,考虑为您希望发布的作品运行一个模拟实验。也许你正在使用C或Java或R或…你希望你的结果是可重复的。这些语言 (以及其他许多语言) 提供了一种 “播种” 其prng初始状态的方法。你以某种方式设置种子或其他,你得到相同的 “随机” 数字序列。Math.random也需要种子,只是没有办法自己设置。Math.random的规范也是相当开放的,允许浏览器供应商使用 “依赖于实现的算法”,只要输出在范围 [0,1) 上近似一致。
从个人的角度来看,我非常喜欢基于浏览器的交互式数据可视化,用于传达数据和概念。这可能包括模拟; 在浏览器中实用是有限制的,但web workers可以提供帮助。模拟经常需要随机数。如果随机数不可再现,则模拟的条件不能重新运行。还有很多其他用例,比如可重复的动画,JavaScript不再只是浏览器的编程语言。
有问题的prng
到目前为止,我已经跳过了均匀分布的prng的工作原理。这一切都像一个黑盒子: 你调用一个函数一次或多次,可能设置一个种子,然后一些伪随机数出来。问题是创建一个好的PRNG是困难的。有成千上万的论文的主题和多种方法。还有很多例子,那些比我更了解这个话题的人似乎做错了。例如…
RANDU
RANDU是IBM 20世纪50年代开发的 “线性同余生成器” (LCG)。LCG使用以下形式的递归关系来生成新的伪随机数:
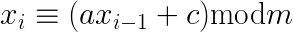
在RANDU的情况下, c为0, a为65,539, m为2 31。由于c为0,因此RANDU是称为 “乘法同余生成器” (MCG) 的LCG子集的成员。要获得0到1范围内的数字 (如Math.random的替换所期望的),只需要将RANDU递归关系的结果除以m。一个JavaScript实现 (你绝对不应该使用!) 可能看起来像这样:
var randu = 函数 (种子) {“严格使用”; if(!isFinite(seed)){抛出新的错误 (“种子不是一个有限的数字”);} var x = Math.round (种子);变量a = 65539;var m = Math.pow(2, 31);如果 (x<1 | | x ≥ m){抛出新错误 (“种子越界”);}返回函数 (){x = (a * x)% m;返回x/m;}; };
由RANDU中的递归关系生成的值的奇偶性永远不会改变。也就是说,奇数种子仅产生x的奇数值,而偶数种子仅产生x的偶数值。这不是一个理想的属性,但还有更大的问题。
LCG的周期最多为m ,但对于RANDU而言,它远小于该周期,并且取决于种子的奇偶性。对于奇数种子,它超过5.36亿,但对于偶数种子,它可以像16,384一样小。
还有另一个理由不为偶数种子而烦恼: 评估生成器随机性的一种常见的简单方法是将连续值对绘制为散点图。一个好的PRNG应该相当均匀地填充一个1 × 1的正方形。有了10,000个随机数,5,000点和1的种子,一切看起来都是合理的。(您可以将 “x” 视为指10,000个随机数的 (0索引) 数组中偶数索引位置的值,即索引0,2,4,6… 9,996,9,998.散点图上的点是通过与下一个奇数索引 (1,3,5,7… 9,997,9999) “y” 值匹配而制成的。)
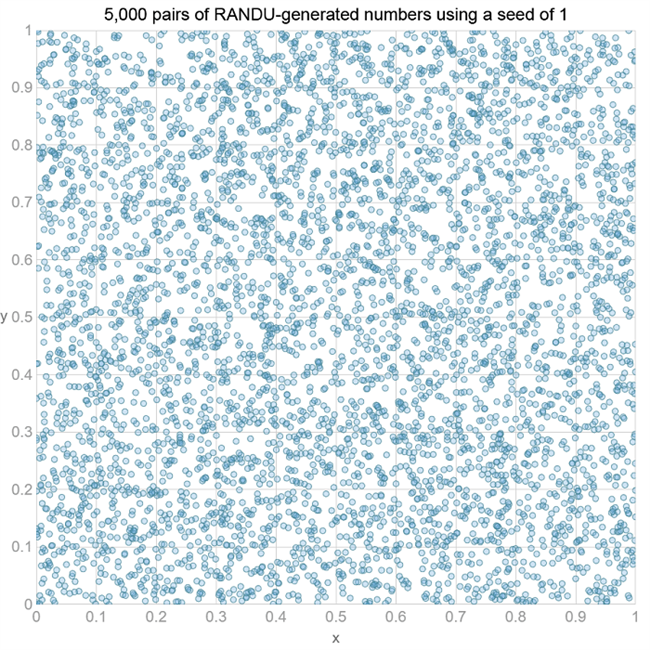
甚至有些种子,我们的东西完全不同。下面是种子32,768的散点图。
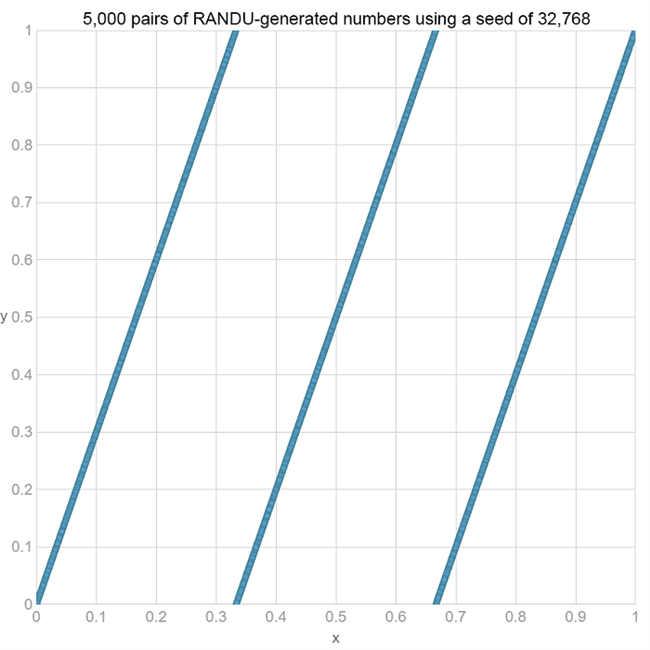
显然,在偶数种子的情况下,我们不仅有不足的分数。在某些情况下,我们在相邻值之间具有明确的关系。
将上面的randu函数调整为甚至拒绝种子,给出适当的错误消息将是足够简单的。不幸的是,赔率种子也显示出结构。要看到这一点,我们只需要通过查看连续随机数的三元组,将散点图的想法扩展到三个维度。3D散点图通常是非常无用的。RANDU数据提供了此规则的例外情况。(此处 “x” 值的索引为0、3、6、9… 9,993,9,996,“y” 值的索引为1、4、7、10… 9,994、9997,“z” 值的索引为2、5、8、11… 9,995,9,998。)
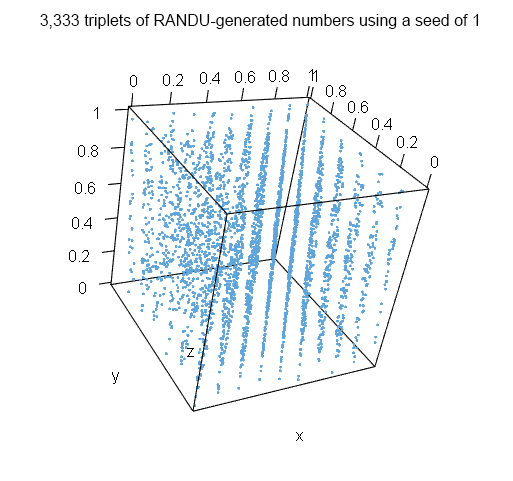
而不是大致均匀地填充盒子,三个数字都位于15个平面之一,无论种子是什么!(实际上,对于偶数种子32,768来说,它比这更糟糕。)我们可以将其与Math.random的结果进行比较 (我为此使用了Chrome); 区别是明显的。
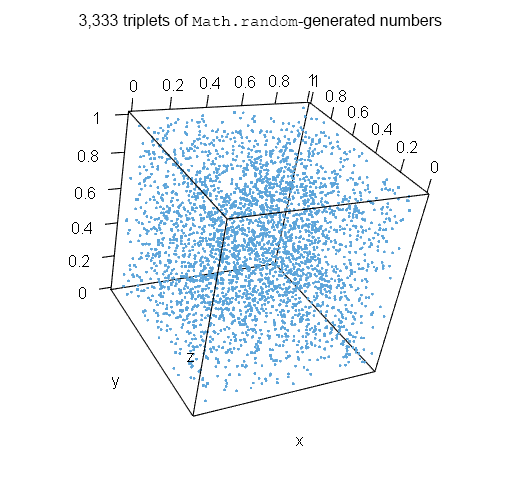
3D散点图的一个普遍问题是图中结构的可见性可能取决于视角。从某些角度来看,RANDU地块中的结构是隐藏的。Math.random可能就是这种情况。为了帮助解决这个问题,我创建了一个交互式版本,让您选择一个PRNG (以及在适当的情况下,一个或多个种子),并使用WebGL可视化结果。这个演示可以找到这里 ,随机数字的盒子可以旋转 (使用鼠标),并从不同的角度观看。在许多浏览器 (Chrome,Firefox,Maxthon,IE,桌面上的Edge和Opera以及iOS上的Safari) 中使用Math.random时,我还没有找到任何明显的结构迹象。
所有MCG都存在3个或更多维度的晶格结构的外观,但对于RANDU来说尤其糟糕。自1960以来就已经知道了。尽管如此,RANDU仍在20世纪70年代中使用,也许应该持怀疑态度地看待那个时代的一些模拟结果。
Excel
您可能想知道PRNG的问题是否仅限于20世纪60年代和70年代?这个问题的简短答案是 “否”。在批评它的旧随机数生成器之后,Microsoft将Excel 2003更改为wichmann-hill PRNG。WH生成器 (于1982首次发布) 结合了三个MCG,以克服单个MCG的一些缺点 (例如相对较短的周期以及在查看相邻值组时看到的晶格平面和超平面)。WH的快速JavaScript实现可能如下所示:
var wh = 函数 (种子) { “严格使用”;if(seeds.length<3){抛出新的错误 (“没有足够的种子”);}var xA = Math.round (种子 [0]);var aA = 171;var mA = 30269;var xB = Math.round (种子 [1]);变量aB = 172;var mB = 30307;var xC = Math.round (种子 [2]);无功aC = 170;var mC = 30323; 如果 (!是有限的 (xA) | |!有限 (xB) | |!有限 (xC)){抛出新的错误 (“种子不是一个有限的数字”);}if(Math.min(xA,xB,xC)<1 | | xA≥mA | | xB≥mB | | xC≥mC){抛出新错误 (“种子越界”);}返回函数 (){xA = (aA * xA)% mA;xB = (aB * xB)% mB;xC = (aC * xC)% mC;返回 (xA/mA + xB/mB + xC/mC) % 1;}; };
同样,我们可以在绘制二维或三维相邻值集时寻找结构:
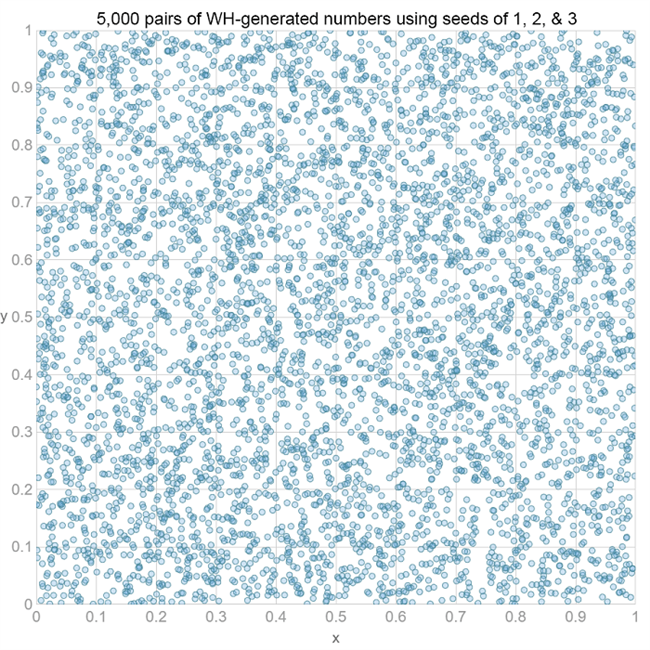
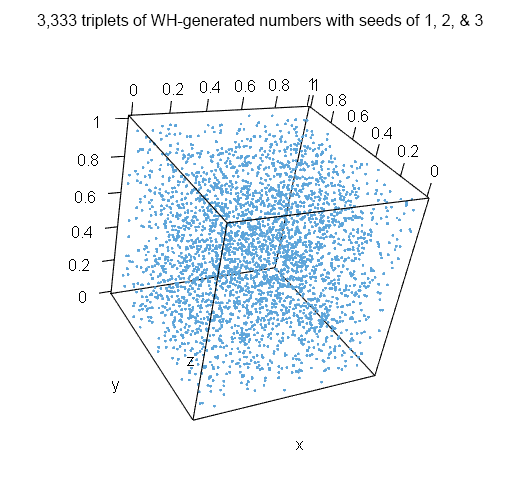
虽然这显然不足以说明我们是否有一个好的随机数生成器,但上面的图至少看起来是合理的。(您也可以在上面提到的WebGL演示中检查三维框。)但是,Excel中RAND函数的WH算法的原始实现偶尔会吐出负数
WH算法未能通过对prng的一系列更现代和更严格的测试,似乎微软已经转向使用流行的 (但更复杂的) Mersenne Twister算法。
V8
前面我使用了Chrome的Math.random实现的输出来说明当绘制为三维散点图时,随机数的三元组的分布应该是什么样子。然而,Chrome的JavaScript引擎V8使用的算法最近被证明是有缺陷的。具体来说,正如这篇冗长但内容丰富的文章所描述的那样,它以比应有的频率高得多的频率复制了相同的 “随机” 字符串。V8开发人员使用迅速更改了算法 ,自49版以来,该问题似乎已在Chrome中修复。
速度
在尝试 “发展自己的” JavaScript PRNG之前,另一个考虑因素是速度。人们应该期望高度优化Math.random。例如,使用几个浏览器的一些非常粗略的测试表明, Math.random在产生100,000随机数方面比上面简单的WH实现快3倍。话虽如此,我们仍然在谈论几十毫秒的顺序 (至少在我的笔记本电脑上的Chrome和Firefox中),所以即使您确实需要大量的随机数,这也可能不是瓶颈。当然,具有更好统计特性的更复杂的prng可能更慢。
结论
我几乎没碰过这里的表面。我只看了几个简单的prng,并表明它们仍然可能是有问题的。还有更复杂的prng算法,其中一些已经通过了大量非常严格的统计测试。其中一些已经有开源JavaScript实现。
如果你不需要重现性, Math.random可以满足你所有的随机数需求。无论哪种方式,如果您的随机数生成器的可靠性对于您的网站功能至关重要,那么您应该执行相关检查。在Math.random的情况下,这意味着检查所有目标浏览器,因为JavaScript规范没有指定供应商必须使用的特定算法。
为您的web应用试用我们的JavaScript HTML5控件,并立即利用其惊人的数据可视化功能。下载免费试用版今天。
