如果您浏览大型印刷报纸并挑选所有图表,您可能会遇到以下一些: 条形图,时间序列 (折线图),饼图,甜甜圈图,堆积面积图。你也可能会遇到奇怪的散点图。如果你在一个美好的一天拿起了《纽约时报》,那么你甚至可能会偶然发现相关的散点图你不太可能找到的是一个盒须图 (又名 “盒图” 或 “盒图”)。相比之下,它们在科学界很受欢迎。
盒子和胡须情节的问题之一,我认为你没有通过媒体进入公众意识的原因之一是,从视觉的角度来看,它们不是特别直观。您可以查看条形图,并立即得到这样的想法,即条形越长,所代表的数字就越大。类似地,我们可以看一个饼图,不经过太多思考就掌握部分到整体的概念,或者在时间序列图中看到一条急剧下降的线,并认为 “这个东西正在迅速下降”。但是箱形图通常是矩形,线和点的混合。然而,我真的不认为它们有那么难理解。当您要比较多个分布时,它们可能非常有用。所以在这篇文章中,我将试图揭开它们的神秘面纱。
我将从一些简单的东西开始,而不是直接使用 “适当的” 盒子和胡须图。下图显示了范围栏的外观和突出部分的标签。正如你所看到的,他们没有太多。您可以使用单变量数据集 ,并绘制一个框来表示最低值和最高值。通常,您还可以添加一条线来指示中值相对于最低值和最高值的位置。
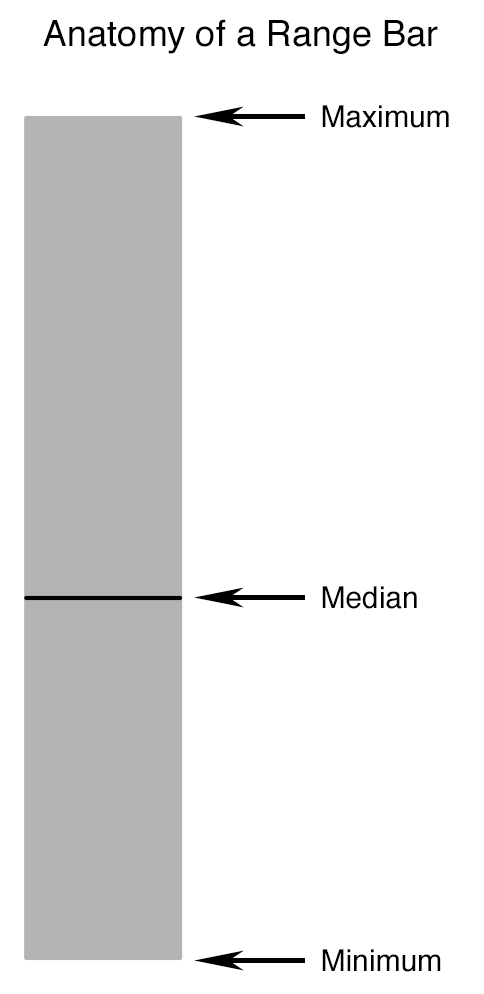
现在,单个范围栏并不能告诉我们很多。如果没有伴随的轴,我们只能判断中位数是否更接近最高值或最低值。你真的不需要一个图表来传达那么少量的信息。将范围条粘贴在刻度上,我们可以估计所有这三个东西的绝对值。但是,范围条及其盒状图表亲的真正力量在于它们如何在不同的单变量数据集之间进行简单的比较。下面的图表说明了我创建的五个任意数据集 (精确的细节在这里并不重要),每个数据集由100个数据点组成。您可以将此布局扩展到十个左右的数据集,没有太大的问题。
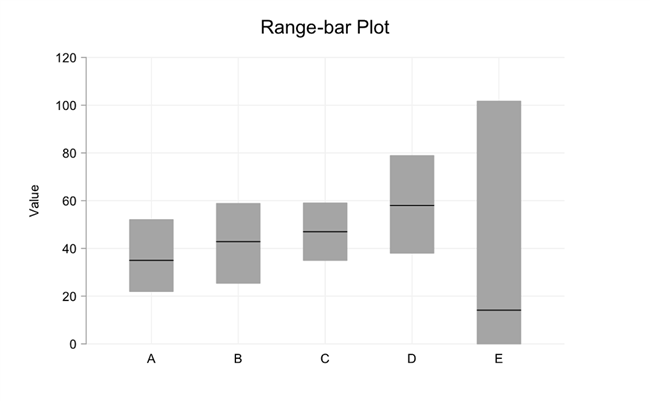
作为一个集合,范围条看起来像条形图中的一组移位条。基本上就是这样。柱越长,每个分布的范围越大。但是,就像我说的,真正的洞察力是从比较酒吧。例如,我们可以看到,数据集E的范围比其他数据集大得多,中位数也低得多。我们还看到,虽然数据集A到D的中位数 (非常) 大致位于它们各自的最小值和最大值之间的一半,但E的中位数更接近最小值。
不久,我将把上面的范围条图变成我所说的简单的盒须图。但首先,这里有一个带标签的图表,说明了一个简单的盒子和晶须的重要部分:
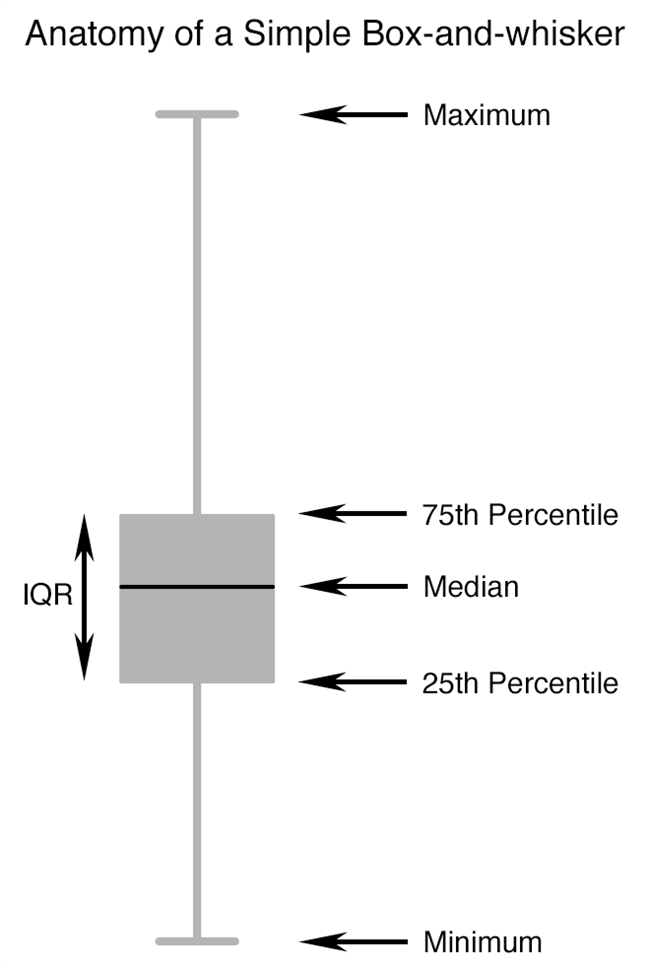
现在,该框仅涵盖50% 数据。在框的上方和下方,我们有 “胡须” 延伸到数据集中的最高值和最低值。25% 数据点具有在框的最小值和底部之间的值,25% 数据点具有在框的顶部和最大值之间的值。这是我之前生成的数据,显示为一组简单的盒子和胡须。
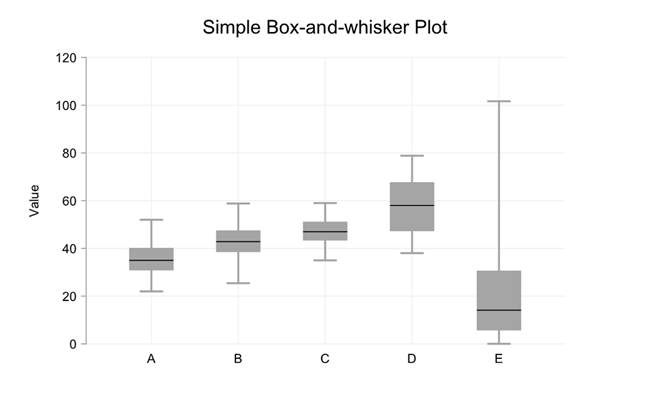
我们现在可以看到,数据集E的大范围主要来自 (最多) 四分之一的数据点- 第75个百分位数比最大值更接近最小值。
盒须图有许多变体试图显示异常值。我最常看到的版本 (我在学校教过的版本) 如下: 而不是胡须必须延伸到最小和最大值,相反,它们延伸到低于/高于第25/75百分位数的最小/最大值,高达四分位数范围 (IQR) 的1.5倍。四分位数范围仅仅是第25和第75百分位数之间的距离。尽管如此,所有这些都是满口的,解释性的图表肯定会有所帮助:
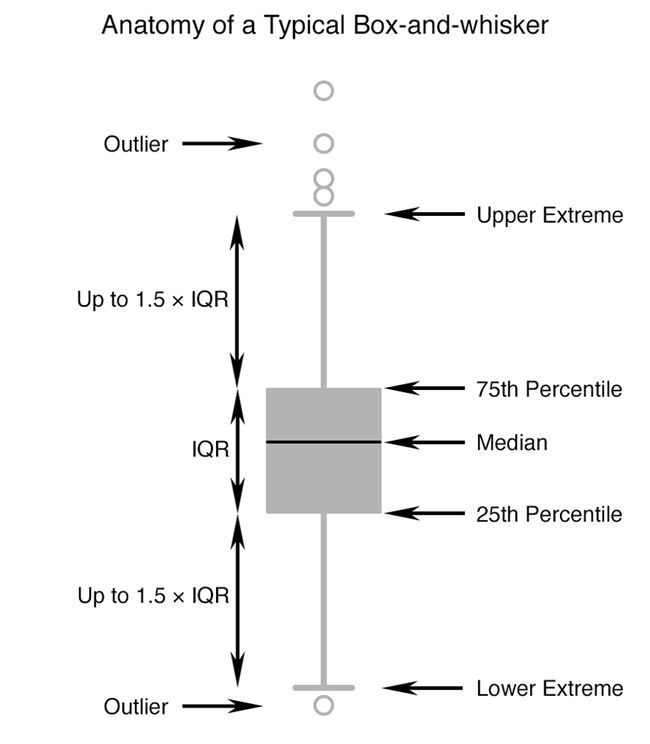
落在胡须的允许范围之外的各个点被明确标记,并被赋予 “异常值” 的状态。(我发现这是 “离群值” 一词的奇怪用法。在其他情况下,“离群值” 是指远离所有其他数据点的数据点。下面的图表使用 “典型的” 盒须图说明了我们的5个数据集。
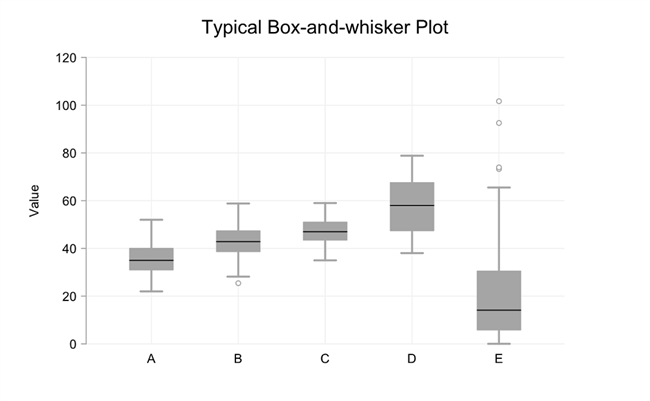
对于数据集A,C和D,简单的盒子和晶须没有变化,因为没有数据点位于25或75百分位数的IQR的1.5倍以上。对于数据集B,有一个点正好低于这个范围。数据集E有四个高度离群值 (两个数据点几乎在彼此的顶部); 尽管E中的最大值大于100,但96% 点低于70。
现在我已经 (希望) 对盒须图进行了神秘化,在第2部分中,我将使用它们与一些现实世界的数据来说明它们的优势。
为您的web应用程序试用我们的jQuery HTML5控件,并立即利用其强大的数据可视化功能。下载免费试用版现在!
